今回は数学的にちょっと難しいお話になりますが、ある質問をあなたにぶつけます。
「ある人が自分と同じ誕生日になる確率は何%であるか答えなさい。」
仮に自分の誕生日が1月1日だとして、目の前にいる人が同じ1月1日の誕生日は何%くらいだと思いますか?
恐らく勝手な想像ではありますが、かなり低そうな数字になるんじゃないかとは想像できるでしょう。
具体的な計算方法と、何人以上集まれば同じ誕生日の人に巡り会う確率が50%になるのか、詳しく調べてみました!
スポンサーリンク
2人の同じ誕生日になる確率の計算!
今目の前に一人の人間がいた場合、その人間の誕生日が同じになる確率は、
1/365=0.274%
さてこの計算を見てもわかるように、相手が自分と同じ誕生日になるということなので、1年365日の内のたった1日になるということです。
365日の中の1日、だから1/365、パーセンテージになおせば0.274%となるわけです。
凄く簡単な計算でしたね。
もちろんこれの逆、すなわち同じ誕生日じゃない確率は、364/365になり、パーセンテージだと99.7%です。
3人の場合は?
さて同じ誕生日になる確率は、2人の場合は0.274%という答えでした。
ではここから少し難しくなります。目の前に1人だけでなくもう1人増えたとして、3人の場合を考えましょう。
目の前に2人の人間がいたとして、その2人とも自分と同じ誕生日の確率はどうなるでしょう?

これは簡単だ、3人だから1/365+1/365で2/365、つまり0.548だ!
と考えるのは全く違います!
2人いた場合の同じ誕生日の確率が1/365だから、人数が1人増えたら足し合わせればいいんだと考えてしまいがちですが、実はこうはなりません。

そもそも2人の誕生日が一致する確率より大きくなるっておかしいよ
これも確率論として少し難しいお話になるのですが、敢えてわかりやすく解説するとしたらこうなります。
目の前にいる人間をAさんとBさんとします。
この時Aさんの誕生日を1月1日とすると、Bさんの誕生日は何パターン考えられますか?

これは……365日じゃない?
はい、その通りです。
Aさんの誕生日を1月1日とすると、同じ1月1日という可能性もあり得るので、1月1日から12月31日までの365日が考えられます。
ではAさんの誕生日が1月2日としたら?
これも1月1日と同じで、やはり同じ1月2日も含んでの365日になります。
これと同じ考えでAさんの誕生日を12月31日まで全て考えた時、その全ての誕生日にBさんの誕生日は365日のパターンが考えられます。
Aさんの誕生日のパターンは365日、Bさんの誕生日のパターンも365日となるので、この2人の誕生日の組み合わせは
365×365パターン
あるのです!
この数字が133,225パターンになるのですが、仮に自分の誕生日が1月1日だったとすると、Aさんの誕生日とBさんの誕生日が1月1日になる組み合わせは
133,225パターンの内のたった1パターンになり、確率は1/133,225となります。
これをパーセンテージになおすと0.00075%、最早宝くじの当選確率並です。
因みに上の計算は、1/365×1/365という計算でも同じになります。要は1人の誕生日が一致する確率を、足し算ではなく掛け算すればいいのです。
少なくとも1人が自分と同じ誕生日の確率は?
さて3人の誕生日全員が一致する確率は、上で求めましたが、次は目の前の2人の内、少なくとも1人の誕生日が一致する確率を考えてみましょう。
またAさんとBさんの2人を例に出して解説します。
自分の誕生日が1月1日とすると、AさんかBさんのどちらか1人が1月1日になればOKです。もちろん2人とも1月1日でもOKです。
そしてこれを求めるには、2人とも誕生日が一致しない確率から逆算するのが早いです。
では2人の誕生日が一致しない確率はどうなるでしょうか?
まず自分の誕生日を1月1日とすると、Aさんの誕生日は1月1日を除いた364日の内のどれかです。
仮にAさんの誕生日を1月2日と仮定したら、Bさんの誕生日は1月1日と1月2日を除いた363日の内のどれかです。
計算式でまとめると、364/365×363/365 となります。
これを計算すると132,132/133,225、パーセンテージだと99.18%になります。
ではこの数値から、少なくとも1人の誕生日が一致する確率を求めます。
実は確率論では、ある事柄について全ての事象の確率を足したら1になるという性質があります。
今回の例で言いますと、目の前の2人の誕生日の全パターンの確率を足したら1になるということです。
そのパターンは以下の2つです。
この2パターンの確率を足したら1になるので、P1+P2=1という計算式が成り立ちます。
そしてP1については上の計算で求めたように、132,132/133,225です。
ではここから少なくとも1人の誕生日が一致する確率は1からP1を引けばいいので、
1−P1 = 1−0.9918 = 0.0082
即ち0.82%が答えとなります。
この1から引いて確率を求める考えを余事象と言いますが、これが次に紹介する誕生日パラドックスでも出てきます。

こうして計算してみると、結構大変だなぁ
誕生日パラドックスとは?
さて今までの解説で、2人ないしは3人集まった時に、同じ誕生日のペアができる確率の求め方がわかったと思います。
でも実はこの議論、更に応用的なお話があるのをご存知ですか?
それが今からお話する誕生日パラドックス(誕生日の奇跡)です!
誕生日パラドックスとは、「ある場所に何人集まれば、同じ誕生日のペアが出来る確率が50%を超えるか?」という命題で、この命題の答えが割と衝撃的なものです。
結論から言いますと、
ある場所に23人集まれば、同じ誕生日のペアが50%の確率ででき、70人集まればほぼ100%同じ誕生日のペアが出来る
が答えとなります。

え?たった23人で50%も?
誕生日のパターンが365日もあるので、にわかには受け入れがたいですよね?
でも上で紹介したのと同じ計算方法で計算すれば、ちゃんとこの数字が導けるのです。
50%の確率で同じ誕生日同士のペアができる人数を求めましょう。
同じクラスに2人の学生がいたとして、その2人の誕生日が異なる確率は、364/365、3人に増えたら364/365×363/365、これは上の式で求めた通りです。
ではこれがN人いる時はどうなるでしょう?
そのN人の誕生日全てが異なる確率は?
っと聞かれたら、そのN人の上限は必ず365となります。
なぜなら366人集まれば必ず同じ誕生日の人が出てくるからですが、誕生日がバラバラとなる確率は上の3人の考えを単純にN人まで拡張して考えます。
N人分全員の誕生日が異なる確率は、分母が365のN乗となり、分子の数は364×363×362×・・・365-(N-1)となるわけです。
これをわかりやすく画像で説明しますと、以下のように階乗を用いた式になります。
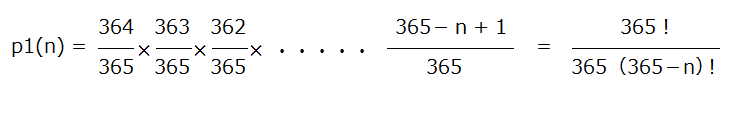
※整数nの階乗とは、1からnまでの全ての整数の積のことで以下のような式で表されます。
n!= n×(n-1)×(n-2)・・・×3×2×1
スポンサーリンク
では本題に戻りますと、求めるべき答えは「同じ誕生日の2人組が存在する確率は?」と聞かれているので、最低1人でも同じ誕生日の人がいればいいわけです。
ここで余事象の考えを使います。
余事象とは全体の確率100%から、事象Aを引いてそうでない確率を求めたものですから、ここでいう事象AとはN人の誕生日全て異なる確率(=p1(n))です。
つまり最低1人でも同じ誕生日の人がいる確率こそ、求める確率となるわけで、全体の確率から事象Aを差し引いてやればいいわけです。
これを方程式で表すと上に示した画像から、
1-p1(n)=「1-364/365×363/365×362/365×・・・{365-(N-1)}/365」=0.5
となります。
あくまで近似的な値ですがこの方程式を解いてやれば N=23 という数字が求められます。
つまり同じクラス内に23人いれば、同じ誕生日同士の組み合わせが出てくる確率が50%となるわけです。
因みに人数と確率の関係は以下のようなグラフで表されます、人数が40人時は確率がほぼ90%になります。
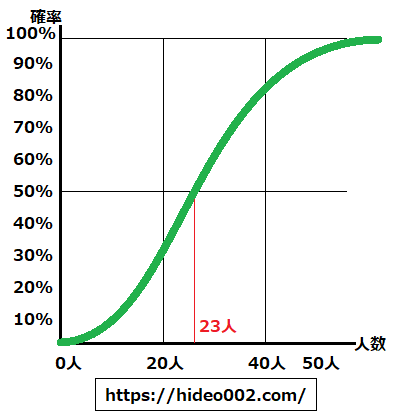
いかがですか?
直感的に求めた回答とかなり違っていて驚いたのではないでしょうか?
これが有名な誕生日パラドックスと呼ばれるものですが、たった23人もいれば同じ誕生日のペアができるのが50%ってうまく納得できないですよね。
けど実際に数学に正しく計算すると、こういう結果になっちゃうんです!
また同じような考えでこれが99%、つまり実質ほぼ100%の確率で同じ誕生日同士のペアが出てくる確率の人数は70人の時です。
つまり70人も集まれば、同じ誕生日の組み合わせが最低1組はいる、と考えて間違いないということになります!

同じ誕生日って言っても、1年365日あるわけですから、普通に考えたら10人、20人なんかで同じ誕生日同士のペアができるなんて考えられないですよね。
そう考えたら50%の確率なんで、まぁ365日のうちの180日分くらいの人数で事足りるんじゃないか、つまりだいたい180人前後かな?
って考えてしまいがちですよね
僕も最初そう考えてました、しかしこれにはある先入観も関係していたのです。
なぜパラドックスと言われるか?
なぜ50%という確率がたった23人という人数で、納得しづらく感じるのでしょうか?
それは多くの人が「自分と同じ誕生日の人がいる確率」と考えていることです。
今回取り上げたのは、あくまで「ある場所に集まった人の中で、同じ誕生日のペアが出来る確率が50%を超えるのは何人からか?」ということですが、わかりやすく言うなら第三者的な視点で捉えていること。
これを主観的、すなわち「自分と同じ誕生日の人がいる確率」と特定してしまうと、また確率が変わってきます。
仮に自分の誕生日が1月1日だとすると、同じクラスに23人いたとしても、その誕生日の人がいる確率はたった5.8%にしかなりません。
これは直感的に理解しやすいですが、どうして値が変わってくるのでしょうか?
それは1月1日以外の誕生日は364/365という確率ですが、これは人数が増えても分子の数は364と変わりません。
つまり「1-(364/365)×(364/365)……」を23人分繰り返すことになります。
364/365の割り算の値は「1」に限りなく近いので、その割り算をいくら掛け合わせても、上記の計算結果はゼロから大きくなるペースが遅くなります。
自分と同じ誕生日の人が少なくとも一人いる確率が、予想以上に大きくなりづらくなり、23人の時の確率は5.8%。
因みにこの計算を用いると180人の時だと確率は約40%。50%とまではいきませんが、やや納得の行く数字になったと思います。
まとめ
今回は誕生日が一致する確率の計算について、2人ないしは3人の時で解説してみました。
その他にも面白い数学系の雑学ネタを書いておりますので、興味があればぜひご覧ください!
【こちらの記事もどうぞ!】
素数が無限に存在することの証明!高校数学の知識と応用編も紹介!
スポンサーリンク

コメント失礼します。
>つまり70人も集まれば、自分と同じ誕生日の人間が最低1人はいると考えて間違いないということです!
70人も集まれば同じ誕生日の組み合わせが最低1組はいる
の間違いではないでしょうか。
同じ誕生日の人間が最低1人いるのであれば、35組の誕生日が同じ組み合わせが出来ていなかればなりません
コメントありがとうございます。
ご指摘の通りで表現で間違いありません、訂正しました。
今後も当ブログをよろしくお願いします。