筆者は高校時代の得意科目は数学でした。
プロフィール欄にも書いてありますが、某国立大学の工学部出身でしたからね。
理系で最重要科目は数学なので、もちろんこれを制覇しないで受験は突破できません。
さて高校数学で学ぶ知識の一つに平均変化率というテーマがあります。
この平均変化率ですが、最初に学んだ時は少しややこしかった記憶がありますね。
例えば「以下の2つの関数で、変数xが1から3まで変わる時の平均変化率を求めなさい。」と言った感じで出題されます。
- f(x)=-3x+9
- f(x)=-5x²+6x+31
高校数学の教科書では定番的な問題かもしれませんが、皆さん求められますか?公式もありますが、実は関数によっては凄く簡単に求められることもできます!
ということで今回は平均変化率の求め方を公式と合わせて、わかりやすく解説していきます。ぜひ参考にしてみてください!
スポンサーリンク
平均変化率の意味とは?
そもそも平均変化率とは何なのか、基礎的な部分から解説していきます。
高校数学で初めて登場する用語で、漢字も5文字あってやや難しく聞こえますが、これは簡単に言えば中学の数学で習った「変化の割合」と同じ意味です。
中学の数学で以下のような問題を解いたことがあるでしょう。
さてこの問題が出題された時に、x座標とy座標の2つの座標の変化分を考慮しますと、
- x:3から10に増加
- y:1から15に増加
となるので、変化の割合は「yの増加量÷xの増加量」と計算して求められます。
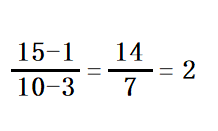
これは言い換えれば「2点間を通る直線の傾きを求めている」ということと同じです。
つまり上の2点間を通る直線の傾きは、以下のような式で表されます。
f(x)=y=2x-5
仮に上の2点の座標を代入すれば
となってx座標の値とy座標の値は確かに一致しますね。
高校数学ではこの変化の割合を、微分という分野で用いるために再登場しました。平均変化率と名前を変えていますが、単純に言葉が難しくなっただけです。
スポンサーリンク
平均変化率の求め方!
では本題の平均変化率の求め方をご紹介していきます。
これについてはまずは簡単にですが、公式をお見せした方が早いでしょう。
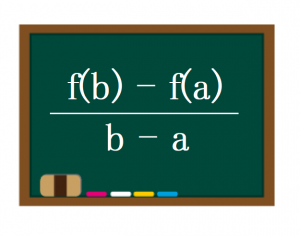
これが平均変化率を求める公式です。
前の章でも紹介しましたが、平均変化率とはグラフの傾きを求めることと同じです。
よって公式は、「y座標の増加量÷x座標の増加量」をそのまま表現した形です。
この公式さえあれば、どんな関数でも平均変化率を簡単に求められます。
ではイントロでも紹介した例題を解いてみましょう。
まずx座標に1と3をそれぞれ代入した時の、y座標を2つ求めないといけません。
- f(1)=-3×1+9=6
- f(3)=-3×3+9=0
よってそれぞれを公式に当てはめますと、
f(3)-f(1)/(3-1)=(0-6)/2=-3
となるので、平均変化率は-3と求められます。
でもここで「あれ?」となりますよね。
気づいた方も多いでしょうが、これって直線の傾きと全く同じ値になっています。
先ほども紹介したように、平均変化率とは変化の割合、つまり傾きと同じなのです。
特に1次関数の一般形は「y=ax+b」となりますが、定数のaが傾き、定数のbが切片となるのは中学数学でも習いますね。
ですのでこの場合は公式に当てはめずとも、xの係数であるaが答えになるので、すぐに-3とわかります。
しかしこれは1次関数のみできることです。
xの次数が2以上になりますと、平均変化率は上で紹介した公式に当てはめて考えないといけません。
2次関数の平均変化率は?
では2次関数の平均変化率を求めてみましょう。
この場合もイントロで紹介した例題で考えることにします。
この問題も[1]と同様で、やはりx座標に1と3をそれぞれ代入した時の、y座標を2つ求めないといけません。
- f(1)=-5×1²+6×1+31=-5+6+31=32
- f(3)=-5×9²+6×3+31=-45+18+31=4
よってそれぞれを公式に当てはめますと、
f(3)-f(1)/(3-1)=(4-32)/2=-14
となるので、平均変化率は-14と求められます。
ここで注意すべきは、平均変化率は直線の傾きと説明しましたが、[1]の時と違ってxの係数が答えにならない点です。
これは2次関数のグラフの形状を見てもらえればわかります。
2次関数の一般形は「y=ax²+bx+c」という式で、以下のようなグラフの形をしています。
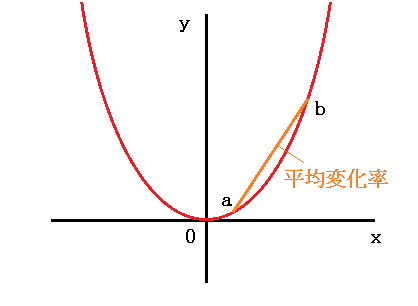
2点(1,32)、(3,4)間の平均変化率というのはこの場合、2点間を通る直線の傾きとなるのです。
しかし2次関数は上の画像のように直線にはならず、曲線ですよね。これが注意すべき点です。
では2次関数の場合で、公式に当てはめず簡単に求められる方法はないのでしょうか?
実はこれについても少し面倒ではありますが、ないことはないです。
まず平均変化率の定義をおさらいすると、
「xの値がmからnに変化した時の、yの変化量をxの変化量で割った数値」でした。
ここでxの値の増加をmからnではなく、mから「m+Δm」と表現することにします。
※Δmとは「n-m」と同じことです。
yの値はそれぞれ、
- f(m)=am²+bm+c
- f(m+Δm)=a(m+Δm)²+b(m+Δm)+c=am²+2amΔm+aΔm²+b(m+Δm)+c
となるので、これを公式に当てはめてみます。

長い手順となりましたが、xがmからm+Δmまで増加する際の2次関数の平均変化率は、最後の赤文字の式で表現できます。
つまり「2am+aΔm+b」となるわけです。
この式に先ほど解いた例題の数値を代入してみます。
例題では、a=-5、b=6、m=1、Δm=3-1=2なので、
平均変化率=2×(-5)×1+(-5)×2+6=-10-10+6=-14
となって、確かに上で求めた数値と一致しましたね!
余裕がある方は、2次関数の平均変化率として上の式も覚えてみましょう。
おまけ:微分係数との違いは?
最後はおまけとして、平均変化率と微分係数との違いについて触れておきたいと思います、
恐らくこの両者をごっちゃにしている人もいるみたいです、僕もそうでした(;^^
微分係数というのはある関数f(x)があった時に、2点(a、f(a))・(b、f(b))間の平均変化率として、bの値を限りなくaに近づけた値という意味です。
式としては極限を用いて以下のような表されます。

図形で表現すると上のようになりますが、点Bの座標(b、f(b))を限りなく点Aに近づけると、直線が点A(a、f(a))の接線になっていくのがわかります。
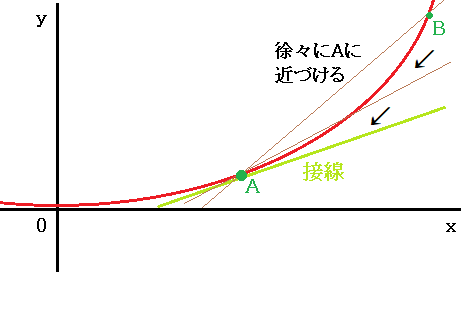
間違っても「平均変化率=微分係数」と勘違いしないようにしましょう!
因みに上の例題で解いた2次関数は、平均変化率が「2am+aΔm+b」となるので、Δmを限りなく0に近づけると「2am+b」となり、これが座標(m,f(m))における微分係数となります。
まとめ
今回は平均変化率の求め方と公式、さらに微分係数との違いについても解説しました。
それでは改めて今回の内容をまとめることにします。
- 平均変化率とは変化の割合、すなわちグラフの傾きと一緒
- 2次関数ではx座標の増加分をΔmとすると、「2am+aΔm+b」という式で平均変化率が求められる
- 微分係数は平均変化率において点Bを限りなく点Aに近づけた時の値で、接線の傾きを表す
平均変化率の考えをしっかり理解しないと、高校数学の微分はおろか大学に入った後の『微分積分学』でも苦労します。
理系の学生の方は特に重要視して受験に臨むようにましょう!
【こちらの記事もどうぞ!】
非ユークリッド幾何学をわかりやすく解説! 平行線が交わるとは?
スポンサーリンク
