学校の数学ではいろいろな立体について学びますね。
筆者は大の数学好きでしたが、空間図形はやや苦手な部類でした。
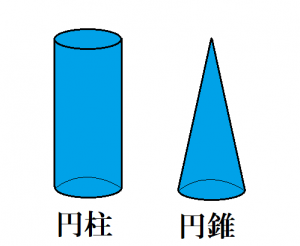
今回紹介するのは底の形が円となっている2つの立体、円柱と円錐です。
両方とも名前に“円”が付いていますが、似ているようで全然違う立体なんです。

円柱と円錐は結局何がどう違うんだっけ?
筆者も初めて学習した時は苦労した記憶があります。同じ円だから親戚なんだろうと、変な感覚で覚えていましたね。
具体的にどういった箇所が違っているのでしょうか?2つの立体について表面積や体積、展開図など詳しく紹介していきます!
スポンサーリンク
円柱と円錐の違いを簡単に!
まずはザックリとですが、円柱と円錐の違いを一言で表現します。
- 円柱とは、底面が円の形をした長い柱、円筒とも言う
- 円錐とは、錐体の一種で底面が円の形をしたとがった立体
ただしこれはあくまでも言葉の意味での違いです。
数学的にはそれぞれ以下のような定義でも正解となります。
- 円柱とは、長方形か正方形を垂直に立てて、垂線を軸として一回転させて出来る回転体
- 円錐とは、直角三角形を垂直に立てて、垂線を軸として一回転させて出来る回転体
※錐体とは簡単に言えば先が尖っている立体の総称、他にも三角錐などがあります。
これを図で表現しますと、以下のようになります。
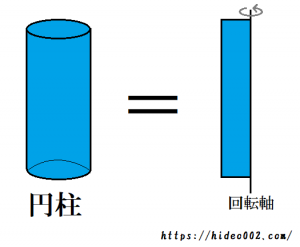
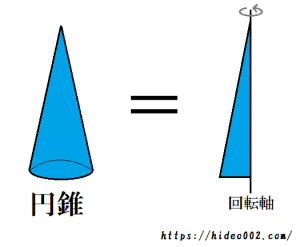
2つとも1つの軸を基準にし、回転させて出来る回転体となります。
回転体ということで、高校数学Ⅲではこの考えを基に体積を求める積分の計算も出てくるんですよ。
だけど難しすぎるので、ココでは省略させていただくことにします。
今回紹介するのは、円柱と円錐の基礎的な知識です。
似たような立体ですが、底面が円なのは共通していて、違いは柱となっているか尖っているかです。
そうなると必然的に展開図や表面積、体積なども違ってくるので、ここからはそれぞれ順番に解説することにします!
スポンサーリンク
展開図の違い!
それぞれの立体の展開図がどうなるのか見ていきましょう!
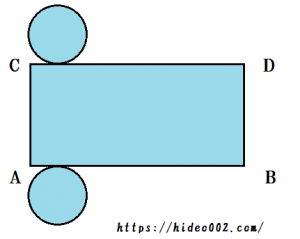
まず円柱の展開図から。
続いて円錐の展開図です。
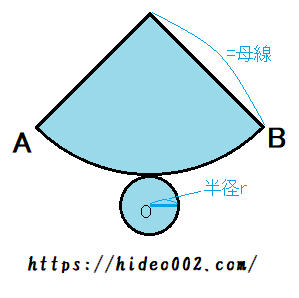
見比べてみるとわかりますが、円柱は2つの円と長方形があり、円錐は1つの円と扇が並んでいます。
そしてそれぞれの図形的な特徴を細かく解説しますと、以下のようになります。
- 円柱の側面の長方形の下辺ABと上辺CDの長さはそれぞれ、底面の円周の長さと等しい
- 円柱の側面の長方形の左右の辺の長さが円柱の高さと等しい
- 円錐の側面の扇形の弧ABの長さは、底面の円周の長さと等しい
これも実際に展開図を組み立ててもらえればわかるでしょう。
長さが少しでも大きかったり小さかったりすると、側面に余分な部分が出来たり隙間が出来て、立体が完成できませんからね。
ここで注意してほしいのが円錐の高さです。
展開図に直すと、扇の一辺の長さ(=母線)が円錐の高さっぽく見えますよね。
だけどこれは扇を円と見なした時の半径の長さに過ぎません。
円錐の高さはあくまで、立体となったときに先の尖っている点から、垂直に下ろした垂線の長さとなります。
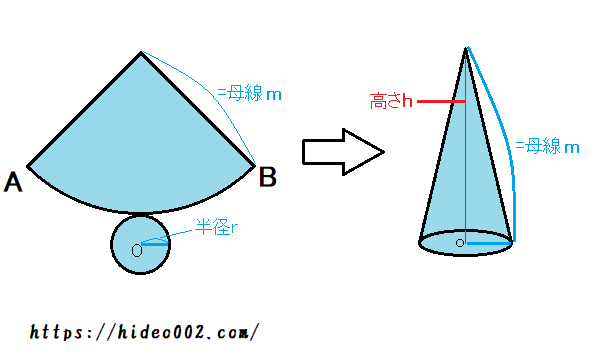
そのため円錐の体積を求める際も、「底面積×母線」にはならないので注意しましょう!
円柱はコンビニで巻き寿司を買う人はよくわかると思いますが、それと全く同じ形状です。
円錐に関しては道路の工事現場でよく見かけるコーンと同じ形です、またアイスのジャイアントコーンとも形が同じですね♪
側面積と表面積と体積を表で!
次に紹介するのは2つの立体の側面積・表面積・体積の公式です。表でまとめましたので紹介します。
わかりやすく円柱と円錐も底面の円の半径をr、高さをhで、同じ長さと仮定します。円周率はπとします。
- 底面の円の半径=r
- 円柱と円錐の高さ=h
- 円錐の母線=m
| 側面積 | 表面積 | 体積 | |
|---|---|---|---|
| 円柱 | 2πrh | 2πr²+2πrh | πr²h |
| 円錐 | πmr | πr²+πmr | 1/3(πr²h) |
それぞれどういった感じで公式が求まるのか、より詳しく見ていきます。
円柱の側面積・表面積・体積
円柱に関しては単純ですね。
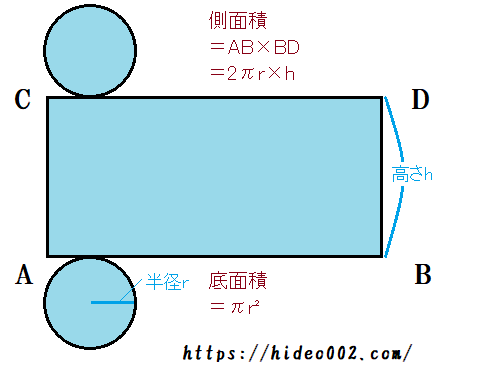
円柱の場合、2つの円の面積と側面積を足せば表面積になります。
円の面積はπr²、側面積は長方形ですが、「円周×高さ」と等しいので、2πrhとなります。
また円柱の体積は、直方体の体積と同様で、「底面積×高さ」でOKです。
よって円柱については、
- 側面積=2πrh
- 表面積=2πr²+2πrh
- 体積=πr²h
となります。
円錐の側面積・表面積・体積
円錐に関しては少しややこしくなります。
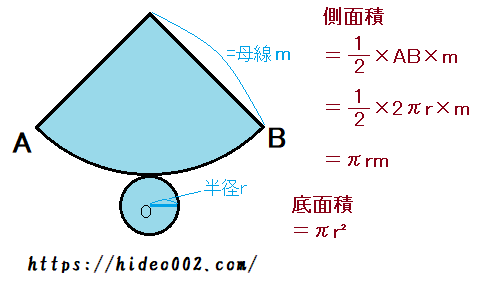
まず側面積ですが、これは母線の長さがmで、扇形の面積になります。
具体的な証明については省きますが、側面積は「1/2 × 弧AB × 母線」となるので、
1/2*(m*2πr)=πmr
となります。
底面積は円柱と同じくπr²なので、表面積=πr²+πmrでOKです。
そしてもう一つ気を付けるべきは、体積が円柱の3分の1になっている点ですね!
実は円錐に限らず他の錐体にも共通している特徴でして、同じ面積πr²の底面を持つ2つの円柱と円錐の場合は、
円錐の体積=1/3*(πr²)*高さh
となるのです。
ではどうして体積が3分の1になるのかですが、これは円錐の型をした容器に水を入れた時を想像すればわかります。
やはり同様に底面の円の面積が円錐と等しい、円柱の容器を用意して、水を満タンに入れます。
そして水を満タンにした円柱の容器から、円錐の容器に水を満タンに移すと仮定すると、ちょうど3杯分で円柱の容器が空になります。
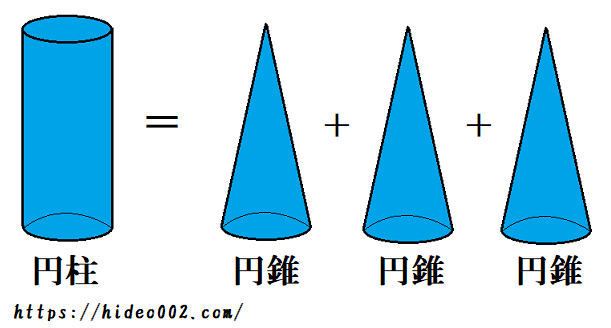
「円柱の中に入った水の体積=円柱の体積」とみなせるので、これが円錐の3杯分でなくなるということは、
円柱の水の体積=3×(円錐の水の体積)
ということが導けます。
よって円錐の体積が、円柱の体積の3分の1になるわけです!
まとめ
今回は円柱と円錐の2つの立体について詳しくまとめました。参考になりましたら幸いです。
言葉の意味だけでなく数学的な意味の方がやはり大事となりますが、展開図と表面積・側面積・体積について詳しく把握できれば大丈夫でしょう。
立体の知識は受験勉強においても重要課題になります。対策怠ると不意打ちを喰らうので、この機会にぜひ覚えておきましょう!
【こちらの記事もどうぞ!】
スポンサーリンク
