小学校の算数では、距離、時間、速さの3つを求める計算を学ぶ内容が出てきます。
距離が「速さ×時間」、時間が「距離÷速さ」、速さが「距離÷時間」となります。
しかしいざ質問された時に、上の3つの求め方を瞬時に出せるでしょうか?

あれ、距離って時間と速さの掛け算だっけ?それとも割り算かな?

確か時間は速さを距離で割ったような?あれ違ったかな?
こんな感じでかなりあやふやになってしまい、結果トンチンカンな回答をする人も少なくないですね。
だけどこれら3つの単位の計算を、簡単に求める方法があるのをご存知ですか?
それが今回紹介する「はじきの法則」と呼ばれる法則です。
小学校の授業で習った人も多いと思いますが、この方法を使えば本当に簡単に計算できちゃうんです。
ということで、今回は距離、時間、速さの3つはじきの法則で求める方法をわかりやすく解説していきます!
スポンサーリンク
はじきの法則とは何か?
距離と時間と速さを簡単に求められる「はじきの法則」とは何なのでしょうか?
実はこの法則は、文章で説明されるものではなく、計算する方法を一目でわかるように図式化されたものとなります。
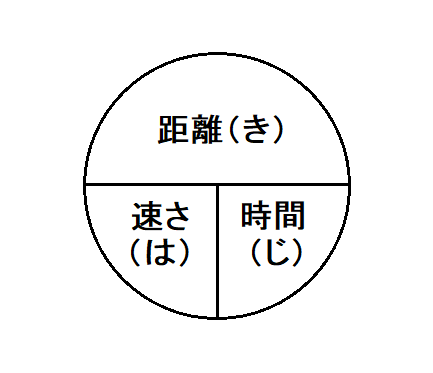
上の画像のように、丸い円を描いて
- 距離を円の上半分
- 速さを円の下半分の左側
- 時間を円の下半分の右側
に位置するように記入して図式化します。
このように書きますと、下の画像のようにそれぞれ3つの単位を掛け算にするか、割り算にするかも凄くわかりやすくなるのです。
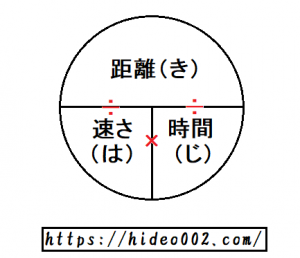
割り算は記号で「÷」ですが、これは「上の数字を下の数字で割る」という意味ですね。
速さと時間はそれぞれ距離を割るということなので、距離が速さと時間の上側に位置して分子、下の2つが分母になるということです。
円の画像では真ん中の横の線が割り算となっているのがわかります。
一方掛け算は記号で「×」で、これは横並びに数字が並びます。
掛け算が登場するのは距離を求める時ですね。
公式は「速さ×時間」なので、上の画像のように下にある縦の線が「×」になり、速さと時間を横に並べる形になります。
スポンサーリンク
はじきの法則を使って求めてみよう!
実際にはじきの法則を使って、3つの単位をそれぞれ求めてみます。
例題として以下のような問題を出します。
- 速さが時速30kmで2時間走行した時の距離は?
- 180kmの距離を2時間30分で走行するのに必要な速さは?
- 200kmの距離を時速25kmで走行した時にかかる時間は?
では順番に見ていきましょう!
1.距離の求め方
はじきの法則より、距離は「速さ×時間」なので、時速30kmで2時間走行した時の距離は
30×2=60km
と簡単に求まります。
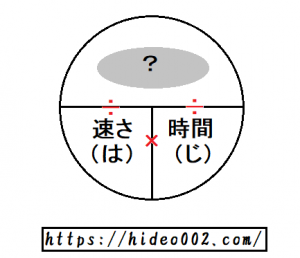
またこの場合上の画像のように、距離の部分を指などで隠してみてください。
そうすれば、下の速さと時間が横並びになっています。
このように距離を求めたい時は、距離の部分を隠すことで、速さと時間を掛け算すればいいとわかります。
2.速さの求め方
はじきの法則より速さは「距離÷時間」なので、180kmの距離を2時間30分で走行するのに必要な速さは
180÷2.5=72km/h
と簡単に求まります。
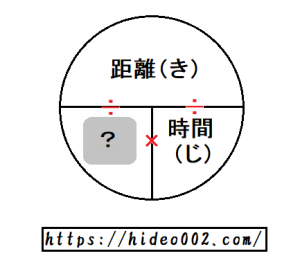
またこの場合もやはり上の画像のように、速さの部分を指などで隠せば、距離と時間が縦に並んでいるのがわかります。
速さを求めたい時は、速さの部分を隠すことで、距離と時間の割り算だとすぐに判別できるわけです。
3.時間の求め方
はじきの法則より時間は「距離÷速さ」なので、200kmの距離を時速25kmで走行した時にかかる時間は
200÷25=8時間
と求まります。
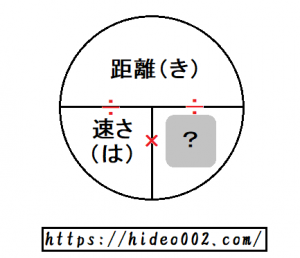
またこの場合もやはり、時間の部分を指などで隠せば、距離と速さが縦に並んでいるのがわかります。
時間を求めたい時は、時間の部分を隠すことで、距離と速さの割り算だとすぐに判別できるわけです。
簡単な覚え方とは?
ここまでの説明ではじきの法則を使えば、距離と速さと時間の3つを簡単に求められることがわかりました。
だけど肝心なのは、このはじきの法則をしっかり頭に入れることです。
実は僕が家庭教師をしていた頃、教え子がこのはじきの法則を勘違いしていたようで、「速さを上側、時間を左下、距離を右下」と書いていました。
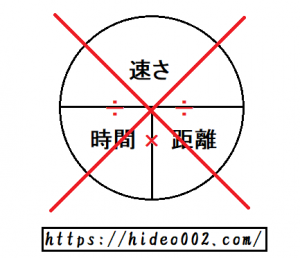
名前が「はじきの法則」ですから、順番通りに解釈すると、ある意味間違えなくもないかなとは思っていました(;^^

うぅーん、実は僕も似たような勘違いをしていたな。
ではこの勘違いを防ぐにはどうすればよいのでしょうか?
対策はいたって簡単で、ある語呂合わせを覚えればいいだけです。
その語呂合わせとは、
木下さん恥を知る
です。
「木」(距離の「き」)の下に、恥(速さの「は」と時間の「じ」)
だから「木下(きのした)さん恥(はじ)を知る」となるわけです。
こうやって覚えれば、距離の下側に速さと時間が左右に並んでいることがすぐにわかります。
「きはじ」や「みはじ」で覚える方法も?
実ははじきの法則には、「きはじの法則」や「みはじの法則」という呼び方もあります。
このような別名があるのは、上でも紹介したように語順通りに覚えられるというメリットがあるからです。
「はじき」という語順だと、どうしても上から順番に「は・じ・き」としてしまいかねません。
でも実際には距離が上で、速さと時間が下側に位置するので、なんとなく覚えづらいという意見もあります。
そのために「木下さん恥を知る」という語呂合わせもあるのですが、別にこんな語呂合わせなんかなくても、
- 上から順番に読んで「きはじの法則」で良い
という方もいますね。
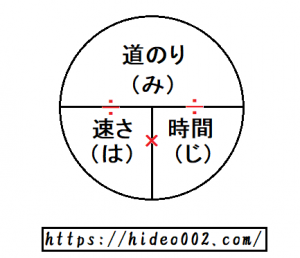
また距離は「道のり」という呼び方もあるので、「き」を「み」に変えて
みはじの法則
という呼び名もあります。
「どうしても語順通りに覚えたい!」という人は、上の2つの呼び方で覚えましょう。ただ個人的には「はじき」というのがしっくりきますけど。

子供のおもちゃで「おはじき」があるから、そっちの方が覚えやすいという大人の配慮かな?
批判もあるのは何故?

このように距離と時間と速さを簡単に求められる優れた法則なのですが、いくつか批判もあります。
例えば
- 「はじきの法則では速さと距離と時間の概念をしっかり理解できない。」
- 「ただ図で理解して、答えを出すことを簡単にする手段に過ぎない。」
という批判です。
昨今子供の学力低下が起きている要因の一つとも言われていて、大学生になっても碌に速さと時間と距離の関係を理解していない人が多くなっているようです。
これについてはある程度納得できる面もあります。
確かにただ図を暗記しただけでは、あくまで公式と求め方がわかるだけで、どうしてそれぞれがそのように求まるのかまで詳しいことはわかりません。
批判が多いのは、学校の教科書や学習指導要領にも載っていないからという見方もあります。
つまり「このように教えてください。」と推奨されているわけではないのです。
あくまで学校のテストでいい点数を取るために、敢えてわかりやすく教えているに過ぎないのです。
改めて正式な定義を解説しますと
速さとは、一定(単位)時間あたりに進む道のり(距離)
となります。
一定時間ごとに一定の速さで進む、だからその掛け算が距離となるんです。
もっと細かい定義については高校数学の微分積分学にまで発展しますが、そこに辿り着くまでには、最低限この考えを理解した方がいいですね。

予備校の教師が、「お前達はいい加減な教え方で学んだな。」とか言ってたっけ。
こういった批判もあるので、極力子供に教える時にも最低限の理屈や定義は交えながら解説してあげましょう。
まとめ
今回ははじきの法則について解説しました。ではおさらいといきましょう。
- はじきの法則は、距離と速さと時間の求め方を図でわかりやすく説明した法則
- 距離を求める時は距離、速さを求める時は速さ、時間を求める時は時間を指で隠せば良い
- 円の上側に速さ、下左側に距離、下右側に時間を配置するように書く、覚え方は「木下さん恥を知る」
習いたての小学生にもすぐに答えを求められるので、覚えておいて損はないです。
ただしあまりに頼りすぎると定義や理屈をしっかり理解しないままになるので、あくまで計算しやすいための手段にすぎないという認識を持ちましょう。
またはじきの法則は高校物理の場面でも、オームの法則を覚える際に役に立ちます。
詳しくは以下の記事をどうぞ!
電気工学において超重要なオームの法則ですが、覚え方がいくつかありました。代表的な語呂合わせと、視覚的に覚える画期的な方法についても紹介しますので、試験対策などにぜひお役立てください!
スポンサーリンク

