円周率
この言葉を初めて聞くのは、学校の算数の授業という人が多いでしょう。
円周の長さ、円の面積、さらに球の体積を求めたり、高校数学ではラジアンと言って角度に変換する際にも使われます。
そしてその円周率の数値は
3.14
というのは有名ですね。
だけどこの数字は実は正確な円周率を表現しておらず、
「3.14159265358979323846264338327950288…」
と言った感じで、小数点以下が無限に続くようになっています。
これではとても計算しづらいので、学校教育では「3.14」と簡略化して計算するようにしています。
果たして円周率に終わりはあるのか?
数学者、及び数学界で昔から提唱されていた謎の一つです。

「円周率に終わりはない」って数学の授業で習った気がするけど、どういうこと?

桁数が何兆とか何京もあるって言われてたけど、本当なの?

終わりのない無限小数ってことは割り切れない数ってこと?
数学でしょっちゅう出てくる円周率ですが、改めて調べると不思議な数だと認識させられます。
今回はそんな円周率の小数点以下がどれだけ続くのか?
また終わりがなければそれをどう証明するのか?詳しく解説していこうと思います。
スポンサーリンク
円周率は終わりのない無限小数!
改めて円周率の定義から解説しますと、円周率とは「円の周長の直径に対する比率」です。
また高校数学からとなりますが、円周率は「π」という記号で表記します。
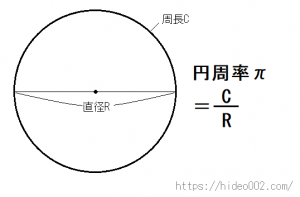
円の周長をC、半径をr(直径が2r)とすると、円周率πは
π = C/2r
という式で表されます。
「円」という図形は、中心からの距離が等しい点の集合を意味するので、この円の周長の直径に対する比率は、半径がどんな値になろうと常に一定です。
一番わかりやすい例だと半径が0.5、すなわち直径が1の時です。
直径が1だと、円周率πは上の式より円の周長と一致します。(π = C)
仮に直径が1cmの円の形をした物体があったとしましょう。
この時の円の周囲を紐で重ならないように巻き、ピッタリの長さでハサミか何かで切り、その紐を一直線に伸ばして定規で測れば、その長さはおよそ「3.14」となります。

でもこの長さはあくまでもおよその数に過ぎません。
冒頭でも紹介しましたが、円周率は小数点以下が無限に続く数です。
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679…
小数点以下100桁まで並べましたが、これよりもさらに延々と続きます。
一体どこまで続くんでしょうか?
むしろ終わりってあるのでしょうか?
答えを言いますと、「終わりはない」です!
スポンサーリンク
円周率の小数点以下の桁数は無限?

実は最新の研究では、円周率の小数点以下の桁数は何十兆という規模にまで膨らんでいたんです!
日本人技術者、円周率を「約31兆桁」計算 世界記録塗り替える
上のニュース記事によれば、何と日本人技術者によって円周率の桁数が31兆まで計算されていました。
31兆といったらもう巨大すぎてわけがわからない領域ですよね(;^ω^)
地球の人口より多いし、宇宙が始まってからの年数よりも長いです。

小数点以下が無限に続くということにあやかって、3月14日に結婚するカップルが多いみたいだね。
このように小数点以下が循環することなく、無限に続く小数となっている数を無理数と呼んでいます。
円周率は紛れもなく無理数ですが、他にも自然対数で習うネイピア数、あと平方数でお馴染みの√2や√3もあります。

√(平方数)って大抵無理数だよね。
ここで無理数と言う言葉が出てきましたが、反対語に「有理数」があります。
有理数とは2つの整数aとbを用いて、「b/a」という形で表される数字のことを指します。
この有理数の最大の性質として、
- 小数点以下の桁数が有限の有限小数
- 小数点以下の数字が循環する循環小数
があります。
①の性質については、一番わかりやすい例が「1/8」、「2/5」、「1/32」などがあります。
それぞれ小数で表すと、「0.125」、「0.4」、「0.03125」と表記され、「割り切れる」というのが最大の特徴ですね。
割り切れるから分数で表現できるわけですね。
また②については、「1/3」、「1/15」などがあります。
これらの数は①とは反対に「割り切れない」数になりまして、小数だと「0.333333…」、「0.07692307692307692…」といった感じで小数点以下が無限に循環します。
ただし無理数とは対照的に、無限に続くと言っても同じ数が一定間隔で循環する特徴があります。
「1/3」であれば、小数点以下がずっと3で続きますし、1/15であれば小数点以下第1位から「076923」でループしています。
このように一定の規則性を保ったまま、小数点以下が循環する数を「循環小数」と言います。
割り切れる数字ではありませんが、循環小数は分子と分母が整数で表現できるので有理数になります。
無理数は非循環小数!
無理数は①と②の両方にも当てはまらない小数です。
すなわち小数点以下が無限に続き、かつ一定の規則性で循環もしない小数となります。
「非循環小数」と呼びますが、円周率の100桁までの数字を見てもらえれば、確かに循環もしていませんね。
もちろんこれよりさらに桁数が伸びたらわかりません。
もしかしたら小数点以下100兆番目とかで、一番最初の数字に戻って循環するかもしれません。
だけど現時点ではそのような気配は全くなく、小数点以下何十兆まで計算しても、一定の規則性はどこにもありません。
もし循環することがわかったら、もう円周率の桁数を計算する必要もなくなります。数学の歴史どころか、世界の歴史をひっくり返すほどの大発見になるでしょう。
にもかかわらず未だに小数点以下何十兆番目まで計算しているのは、やはり円周率が非循環小数だからです。
それこそまさに「神のみぞ知る」ということになりますね。
円周率が無理数であることの証明!
円周率が、小数点以下が無限に循環せず続く無理数だとわかったわけですが、そもそもどうしてこんな数になるのか不思議に思いませんか?

円周率って円の周長と直径の比だけど、それが無理数になるってどうもしっくりこないな。
実は円周率が無理数であることは、古代エジプトからも知られていたようです。
古代の幾何学者達は円周率は円の大きさに寄らず一定の値で、それが3より少し大きい程度だとは知っていました。
ただしその正確な値までについては当時は知るすべはなく、紀元5世紀の中国の数学者によってようやく小数点以下第6位まで推算されました。
また小数点以下第6位(3.1415927)まで求めたことで、その近似値も「22/7」という有理数であることも算出しました。
もちろん「22/7」というのはあくまで近似値に過ぎないので、円周率が無理数でないとは言い切れません。
円周率が無限に続く数である事実については、その証明が割と難しいことで有名です(汗)
正直理数系の大学で習う超難しい内容に近くなるため、ここでは敢えて簡単に解説することにします。
下のように直径1の円を描き、その中に正n角形を内接するように描けばイメージが付きやすいでしょう。
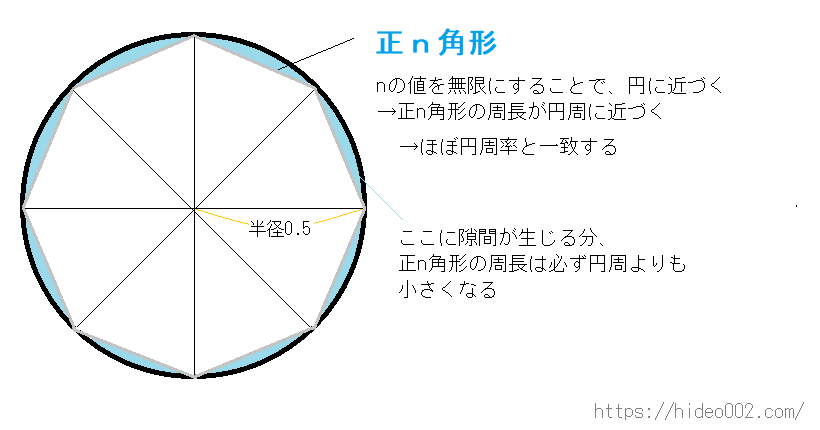
今ではコンピュータの計算のおかげで、円周率πはかなり正確な値を求めることができます。
でも昔の人達はコンピュータもありませんから、このように図形を用いて円周率の長さを求めていたわけですが、ここで注目してほしいのは正n角形の周の長さです。
ではどのようにして計算していったのか、正六角形の例から順番に解説していきましょう。
円に内接する正六角形で考えよう!
最も分かりやすい例が正六角形の時です。
実はこの正六角形を使えば、円周率が3よりも大きい数字であることが証明できます。
正六角形は下の画像のように、全ての辺の長さが円の半径と等しくなります。
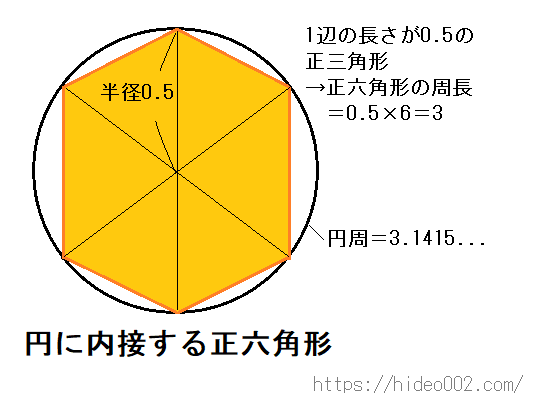
正六角形を構成する六つの三角形が正三角形になっているから、おのずと導ける性質ですが、この性質により、正六角形の外周の長さは円の半径の6倍になることもわかります。
つまり円の半径が0.5cmならば、0.5×6で3cmとなります。
そして円の半径が0.5cmということは、直径が1cmで円周率は周長と一致します。
これにより「正六角形の周長=3 < 円の周長=円周率」であることも導けて、円周率が3よりも大きいことがわかりました。
ただ見てもらえればわかりますが、正六角形と言うのは円の形と程遠いです。
これは逆に言えば、「円周率=3」と近似するのは、かなり無理があるという見方もできます。

昔ゆとり教育で「円周率を3とする」と言われていたけど、それって円周率を円周率とみなしていないようなもんだね。
正六角形では駄目なので、それよりも頂点の数が多い正多角形で考える必要が出てきます。
正十二角形で考える!
次に頂点の数を2倍に増やした正十二角形で考えます。同じく円の直径は1(半径0.5)とします。

ご覧のように、だんだん円の形に近づいていきましたね。
ではこの正十二角形の外周の長さはどうなるのでしょうか?
こちらは正六角形の時と同じように、単純にはいきません。
まず正十二角形は中心から各頂点に辺で結ぶと、12個の二等辺三角形が出来ます。
この二等辺三角形の二辺は円の半径と同じなのでその長さは0.5、そして円の中心を含む頂点の角度は30度となります。
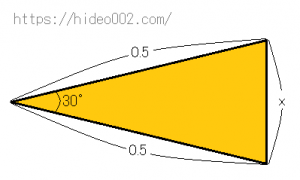
※角度が30度になる理由は、360度から頂点の数12で割ることで求まります。
さてこうなると気になるのが、外周を構成する底辺の長さですね。
この底辺の長さですが、実は高校数学で習う余弦定理が必要になります。
余弦定理とは、下のような三角形ABCがあった時に、角度αと2つの辺aと辺bの長さが決まれば、辺cの長さが決まるという定理です。
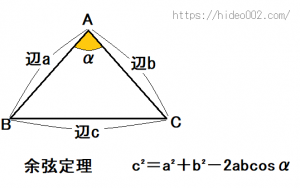
辺cは「c²=a²+b²-2abcosα」となります。
この公式を使うことで、上の二等辺三角形の外周を構成する一辺の長さが求まります。
求めたい辺の長さをxとすると、2つの辺の長さは0.5、角度が30度なので、
x²=0.5²+0.5²-2×0.5×0.5×cos30°
※cos30°=√3/2です。
x²=0.5-0.5×(√3/2)=0.5×(1-√3/2)=0.25×(2-√3)
x=0.5×√(2-√3)
と求まります。
ここで正十二角形の外周は12辺あるので、xを12倍すれば外周が求まります。
よって「正十二角形の外周の長さ=12x=6×√(2-√3)」となります。
√が2つも出てきて凄くややこしいですが、関数電卓を用いて厳密に計算すれば上の値は
- 2-√3=0.26794919
- √(2-√3)=0.51763809
- 6×√(2-√3)=3.105828541
とそれぞれ求まります。
一番下の「3.105828541」が正六角形の周長です、かなり3.14に近づいてきましたね!
だけどこれでもまだまだ不十分で、0.035ほどの誤差があります。
正十二角形程度では、外周を構成する辺と円との間に僅かな隙間がありますから、その分のズレはどうしても生じてしまいます。
無限正多角形で円周率は求まる?
このように頂点の数が増えれば増えれるほど、その正多角形の周長は円周率に限りなく近づいていきます。
この性質を利用し、頂点の数、すなわち正n角形においてnを無限にすると、正n角形が円の形に近づき、「正n角形の周の長さ=円周」となっていくのがわかります。
しかしこれはどう考えても不可能です!
現実的に「周の長さ=円周」となることはなく、あくまで近似値にしかなりません。
改めて言いますと、nは無限大です。
仮に「n=10000」の時は正1万角形となり、ほぼ円の形と等しくなります。
だけどあくまでほぼ等しくなるだけで、完全に一致することはありません。
正多角形はどれだけ頂点の数が増えても所詮多角形です。完全な円にはなりません。
無限大の数字には終わりはないので、正n角形の周の長さは限りなく円周率に近づくだけで、永遠に一致しません。
このようにして考えてもらえれば、円周率の桁数に終わりはないということがなんとなくイメージできるでしょう。
因みにもっと数学的に厳密な証明が知りたいという方は、以下の動画をご覧ください。
難しい数式や公式などが出てきてかなり複雑です、理数系に進む学生なら参考になると思います。
※円周率はあの探査衛星はやぶさの帰還にも貢献していたんです。詳しくはコチラの記事をどうぞ!
小学校で学習した算数の円周率。3.14という数字でお馴染みですが、実は無限に続く小数なのです。調べてみると、0が12個連続で並んだり、9が連続で並ぶポイントもあります。また小惑星探査はやぶさが地球に帰還した際もこの円周率の計算は鍵となったのです。
まとめ
今回は円周率の終わりについて深く解説してきました。参考になりましたら幸いです。
円周率が割り切れない数だなんて、何と言うか人生と同じような感じですね。
どこまでも円周率って本当に不思議で驚かされます、やっぱり数学って奥が深い!
その他数学に関する面白い話もあります。興味のある方はぜひご覧ください!
みなさんが今まで学んできた数学はユークリッド幾何学の世界の話でしたが、その常識が通用しないのが非ユークリッド幾何学の話です。この非ユークリッド幾何学では平行線が交わり、三角形の内角の和も180度とはならず、二角形という図形も描けます。
スポンサーリンク


