今回は知る人ぞ知る有名な確率論のある問題について紹介したいと思います。
その名もモンティ・ホール問題です!
アメリカのゲームショー番組が元ネタとなった問題ですが、数学者の間で議論が沸騰したようです。一種の心理トリックともとれる問題で、普通に考えた時の確率とはまた違った答えとなるので面白いですよ!
スポンサーリンク
1.モンティ・ホール問題とは?
まず下の画像をご覧ください。
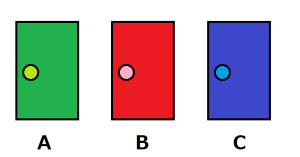
というクイズ問題、よくありがちな奴ですね。もちろんこれには必勝法はありません、当たる確率は純粋に3分の1です。
しかしこのクイズ番組の司会者は意地悪です。
もしもあなたがAを選んだとしましょう。すると、
と言って、その司会者はBのドアを開けました。
すると残ったのはAとCの内のどちらかです、司会者が改めて問います。
この問題ですが、数学で言うところの確率論の話になりますね。
アメリカで有名になったモンティ・ホールという司会者が元ネタとなった問題ですが、大学で確率論を学んだ人なら聞いたことはあると思います。
この問題の一番の核心部分は、確率が、ドアを開ける前と後で変わるかどうか?が問われている所です。
ドアを開ける前は、もちろん3分の1です。しかし外れのBのドアを開けた直後、残り2つのドアの内当たりはどちら、変えた方がいいのか?と考えてみたくなります。
もし開ける前と同じ3分の1であるなら、ここで答えを替える必要はないですね。「いや変えない、自分の直感を信じる!」と自信があるなら、もちろんそのままAのままでいいでしょう。
しかし!
実は詳しい計算の結果、外れのBのドアを開けた後でCに変えれば、当たる確率は3分の2と増えるのです!
「そんな馬鹿な!」と考えてる方も多いでしょう。
確かに普通に考えたら、ここでCに変えたほうが当たる確率が増えるだなんて考えにくいでしょう。しかしこれもある意味錯覚なのです。
スポンサーリンク
2.なぜ当たる確率が増えるのか?
実際に数学的に計算してみるとわかりますが、ここで確率を求めるにはベイズの定理という理論を使う必要があります。
しかしここでベイズの定理を使って説明しても難しすぎるので、簡単に、直感的な説明にとどめさせていただきます。
まず、当たりがA、B、Cの3パターンで考えてみます。
3パターンありますが、最初に自分が選ぶドアはAで固定するとします。ここでA、B、Cの3パターンについて考えます。
まず当たりがAの時
自分が選んだドアもAなので、この時点で当たりです。司会者がBとCどちらのドアを開けようと、変えなければ正解のままです。
次に当たりがBの時
自分が選んだドアはAなので、司会者が開けるドアはCになります。ここではBに変えたほうが正解になりますが、変えなければ不正解のままです。
最後に当たりがCの時
司会者が開けるドアがBになるだけで、結果は当たりがBの時と変わりません。Cに変えれば正解、変えなければ不正解のままです。
以上3パターンについて解説していきました。
ここで気づくと思いますが、それぞれの3パターンでは最初に選んだAのままだと、当たりがAの時しか正解できません、故に正解できる確率は3分の1。逆に変えれば、当たりがA以外の3分の2で正解ということになります。
つまり決断を変えれば3分の2という確率で正解できるということです、このように順序立てて説明すれば、正解する確率は、ドアを変えたほうが上がるということが分かると思います。
3.もしもドアの数を100に増やしたら?
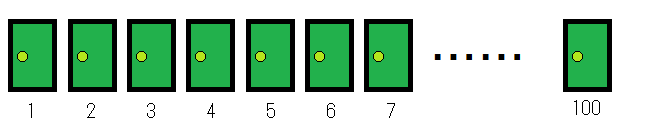
ここではドアの数が3つだけという仮定で説明しましたが、もしもドアの数を100個まで増やしたとしたらどうでしょう?
目の前にドアの数が100個あって、当たりが1個だけの時、その内の一つをランダムに選択すると当たる確率は100分の1です。
やはり司会者が同様に、外れのドアを次々に開けていったとします。1つ、2つ、3つ… と開け続け、最終的に残ったのは、当たりか外れのドア、つまり98個のドアが開けられたのです。
100分の98が開けられ、残り2つのドアの内どちらか1つ、しかもどちらかは最初に自分が既に選んでいます。これを頭の中でイメージできていれば、圧倒的に最初の決断を変えたほうがいいということがわかりますよね。
なぜなら、最初に自分が選んだのは、あくまで閉じられている100個のドアの内のランダムで1個です。残ったドアは99個あって、その内98個は外れとわかりました。
勿論司会者は正解のドアを知っています、となれば一目瞭然でしょう。残ったドア99個全て外れという確率の方が圧倒的に低いのですから。
因みにこのモンティ・ホール問題で確率が高くなると証明したのは、アメリカに住むコラムニストで世界最高のIQ女性といわれるマリリン・ボス・サバントさん。そのIQ値は228でギネスにも認定されています。
今回のモンティ・ホール問題で彼女が示した解答には、著名な数学者も反論しましたが、後にコンピュータによる実験でマリリンの正しさが証明されたそうです。
スポンサーリンク

モンティ・ホール問題に、ベイズの定理を用いるのは間違いです。