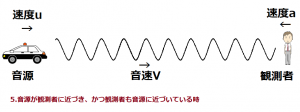
パトカーや救急車が自分がいる場所に近づいてくると、サイレンの音がだんだん高くなっていき、遠ざかっていくと低くなっていきます。
これは一体どういうことなのでしょうか?
普段からよく体感することですが、改めて考えると不思議な現象ですよね?
実はこれには音波のある法則が関係していました。
ご存知の方も多いと思いますが、ドップラー効果と呼ばれる現象です。高校の物理の授業でも習うと思います。
しかし学校の授業で習ってもイマイチわかり辛い部分は多いと思います、特に公式の部分が(;^^)
そこで今回は図を用いて筆者なりにわかりやすく解説していきます。またドップラー効果を応用した技術についても紹介しますのでぜひご覧ください!
スポンサーリンク
音が伝播する原理
ドップラー効果について解説する前にまず音が伝搬する仕組みについて改めて解説します。
我々が普段から耳にする音というのは正確に言えば、物体が振動した時に波として伝わりそれが耳の中にある鼓膜を振動させることで感知しています。
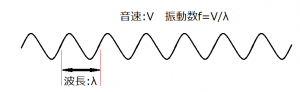
音とはこういった波うった形をしています。
この時1秒間にf回振動させると音源からは振動数fヘルツの音波が出ます。
また音速をV(一般的には340m/s)とすると、波長λは以下のような式で表されます。
λ=V/f
まずはこの基本形をしっかり頭にいれておきましょう!
※音波に関しては以前でも当ブログで取り上げたことがあります、ヘリウムガスを吸うことで声が高くなる原理を解説した記事ですがよければご覧ください!
ヘリウムガスで声が高くなる理由を音の振動数・速さ・波長で解説!
スポンサーリンク
ドップラー効果の公式を解説!
改めてドップラー効果について解説しますと、音源または観測者が動くことで観測者に聞こえる音の振動数が大きくなったり小さくなったりする現象です。

一般的に我々が普段耳にする音というのは、音源が動かないパターンの方が多いです。
しかしドップラー効果では上の図のように音源または観測者が動いた条件の下でどうやって振動数が変化するかを見定める必要が出てきます。
つまりドップラー効果の音波の振動数は、
- 音源が観測者に近づく時
- 音源が観測者から遠ざかる時
- 観測者が音源に近づく時
- 観測者が音源から遠ざかる時
この4パターンでそれぞれ違った公式になるということです。
複雑のように見えますが、先ほど紹介したf=V/λ(以降は本式を①式とする)という基本形さえしっかり頭に入れておけば難しくありません。
それぞれのパターンで振動数を順番に求めてみます。
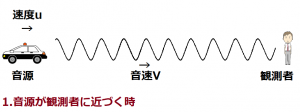
1.音源が観測者に近づく時
音源が一定の速さuで静止している観測者Aに向かって近づいてきていると仮定します。
この時の波長λ1は、上の図のように音源の速度uの分だけ押し縮められ短くなります。また①式から
λ1=(V-u)/V × λ → λ1=(V-u)/f
となるので、これを上に紹介した①式に代入すると、振動数f1は
f1=V/λ1 = Vf/(V-u)
となります。これが音源が観測者に近づく時の振動数f1です。
この場合は分母の値が小さくなるので振動数f1は大きくなります、故に音が高く聞こえます。
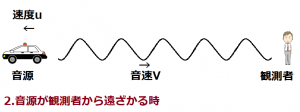
2.音源が観測者から遠ざかる時
音源が一定の速さuで静止している観測者Aから遠ざかっていると仮定します。
この時の波長λ2は、上の図のように音源の速度uの分だけ引き伸ばされ長くなります。また①式から
λ2=(V+u)/V × λ → λ2=(V+u)/f
となるので、これを上に紹介した①式に代入すると、振動数f2は
f2=V/λ2 = Vf/(V+u)
となります。これが音源が観測者から遠ざかる時の振動数f2です。f1との違いは音源の速度uをプラスしているだけです。
この場合は分母の値が大きくなるので振動数f1は小さくなります、故に音が低く聞こえます。
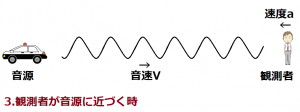
3.観測者が音源に近づく時
観測者が一定の速さaで静止している音源に近づいていると仮定します。
この時は音源から発する波長には何も変化がありません。
変化があるのは観測者と音源の相対速度です。近づいているので観測者は音源に-xの方向に動いていると考えられます。つまり相対速度V1は
V1=V+a
となります。
これを①式に当てはめると、振動数f3は
f3=V1/λ = (V+a)/λ = (V+a)f/V
となります。これが観測者が音源に近づく時の振動数f3です。
この場合は分子の値が大きくなるので振動数f1は大きくなります、故に音が高く聞こえます。
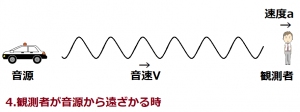
4.観測者が音源から遠ざかる時
観測者が一定の速さaで静止している音源から遠ざかっていると仮定します。
この時も音源から発する波長には何も変化がありません。
変化があるのは観測者と音源の相対速度です。遠ざかっているので観測者は音源に+xの方向に動いていると考えられます。つまり相対速度V2は
V2=V-a
となります。
これを①式に当てはめると、振動数f4は
f4=V2/λ = (V-a)/λ = (V-a)f/V
となります。これが観測者が音源から遠ざかる時の振動数f4です。f3との違いは観測者の速度aをマイナスしているだけです。
この場合は分子の値が小さくなるので振動数f1は小さくなります、故に音が低く聞こえます。
以上がドップラー効果の4パターンの振動数の公式です。
ご理解いただけましたか?
気を付けるべきは、3と4のパターンだけ波長ではなく相対速度で振動数を求めるということです。
応用:2パターンが混在したら?
では1~4のパターンでもしも2つ以上のパターンが重なったらどう求めればよいのでしょうか?
具体例として挙げるなら以下のようなパターンです。
音源が観測者に近づき、かつ観測者も音源に近づいている時の振動数f5は?
これは言ってみれば1と3のパターンが両方重なったと思えばいいだけです。
ゆえに振動数f5は以下のような式で表されます。
f5=(V+a)/(V-u)× f
つまり分子は観測者の速度aの分だけ加算され、分母は音源の速度uの分だけ減算するということになります。
こういった応用パターンで出題されるケースは多いのでしっかりと頭に叩き込んでおきましょう!
おまけ:スピードガンはドップラー効果の応用?
ドップラー効果は野球でピッチャーの球速を計測するスピードガンにも応用されているようです。

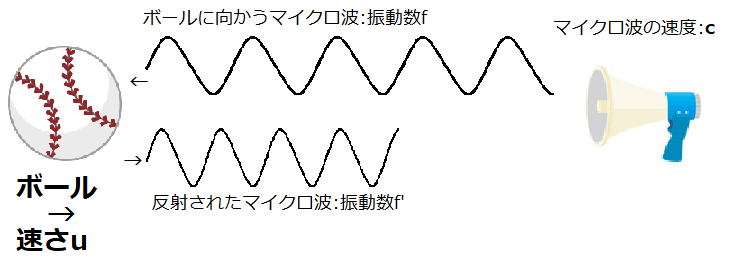
スピードガンの原理を簡単に解説しますとピッチャーが投げた球に対して、振動数がわかっているマイクロ波を射出します。
球に当たり跳ね返ったマイクロ波はスピードガンに戻ってきますが、この時のマイクロ波は最初に射出した時よりも縮んでいるはずです。
マイクロ波の速度をc、球速をv、最初のマイクロ波の振動数をf、跳ね返った後のマイクロ波の振動数をf’とすると、
f’=(c+u)/(c-u) × f
になるので、この振動数の差から球速を算出しているということになります。
まとめ
以上ドップラー効果の仕組みと公式についての解説でした!
ドップラー効果は高校物理だけでなく大学に入った後も波動の授業で必ずと言っていいほど出てくる内容です。
また天文学分野でも宇宙が膨張する原理として説明できるみたいです、詳しくは以下の記事からどうぞ♪
宇宙は膨張を続けている?根拠はドップラー効果にある?
こちらの記事もどうぞ!
フィギュアスケートの回転が速くなる理由を角運動量保存則で解説!
スポンサーリンク