円周角の定理と言えば中学校の数学の図形で習う重要な定理ですね。
この定理を簡単に説明しますと、
「ある円があった時に任意の弧に対する円周角の大きさは、その弧を含む扇形の中心角の大きさの半分になる」
というものです。
高校入試でも出題される超重要な定理なのですが、改めてこの定理が何故成立するのでしょうか?
実はこの定理は逆も成立するのですが、詳しく把握できているでしょうか?筆者自身もこの定理の証明や逆で苦戦した記憶があります。
大抵は角の大きさを求める問題ばかりですが、もしかしたらその証明が実際の入試でも直接問われる可能性も捨てきれないので、今回は念入りにかつわかりやすく解説していきます!
スポンサーリンク
円周角の定理の証明は3パターン!
まずは円周角の定理についておさらいしておきましょう!
※円周角と中心角を間違えないように気を付けてください!
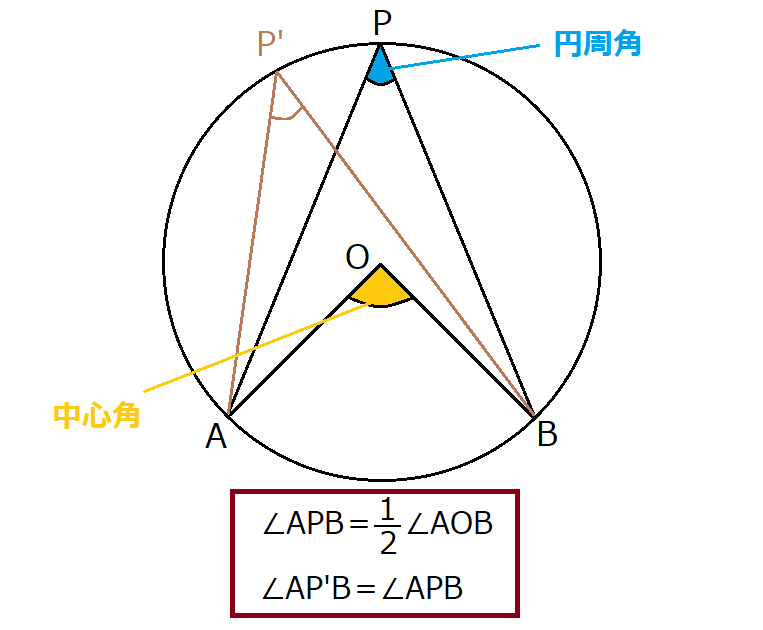
そして円周角の定理とは、以下の2つの性質を満たす定理となります。
- 円周角∠APBの大きさは中心角AOBの半分になる
- 同じ弧に対する円周角の大きさは全て等しい
∠APB=1/2∠AOB
∠AP’B=∠APB
定理1も重要ですが定理2もかなり重要です。要は弧ABに対してどの位置に点Pをとっても円周角の大きさは変わらないのです。
ではなぜこの定理が成り立つのか?その証明には大きく分けて以下の3パターンあります。
- AP(またはBP)が円の中心を通る場合
- 円の中心が円周角の内部にある場合
- 円の中心が円周角の外部にある場合
では順番に紹介していきます!
APが円の中心を通る場合
このパターンの証明は非常に単純です。周上の点Pから結んだ線分APまたは線分BPが、ちょうど円の中心を通っているということなので、以下のような画像になります。
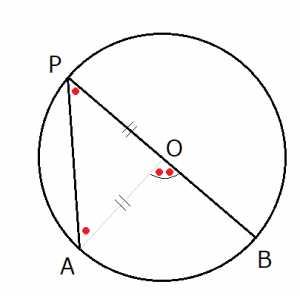
この証明では三角形の外角定理を用います。
外角定理とは簡単に言いますと、三角形の1つの外角はそれと隣り合わない2つの内角の和に等しくなる定理のことです。
上の画像では△APOの外角∠AOBが、2つの内角∠PAOと∠APOの和に等しいので、
∠AOB=∠PAO+∠APO…①
となります。
さらにOは円の中心なので、AOとPOは円の半径で等しくなります。
すなわち△APOは二等辺三角形なので
∠APO=∠PAO…②
となります。
よって①式と②式で、
∠AOB=2∠APO
∠AOBが中心角、∠APOが円周角なので、定理1が証明できました!
円の中心が円周角の内部にある場合
この証明では以下のように点Pから点Oにかけて直線を引き、中心角及び円周角を2つに分けて考えます。
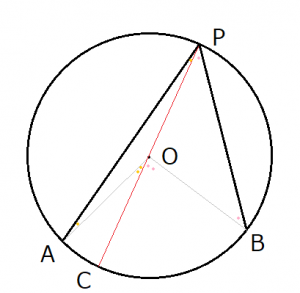
上の画像より△APOと△BPOの2つの三角形に分けられます。また線分POの延長線と円周との交点をCとします。
まず△APOで外角定理を用います。この場合は先ほどの「APが円の中心を通る場合」の証明と全く同じで
∠APO=1/2∠AOC…①
となります。
同様に△BPOでも外角定理を用いれば、
∠BPO=1/2∠BOC…②
となります。
円周角の∠APBに関しては、①式と②式より
∠APB=∠APO+∠BPO=1/2∠AOC+1/2∠BOC=1/2(∠AOC+∠BOC)…③
となります。
さらに中心角の∠AOBに関しては、
∠AOB=∠AOC+∠BOC…④
なので、これを③式に代入すれば
∠APB=1/2∠AOB
円周角が中心角の半分になっているので、同じく定理1が証明できました!
円の中心が円周角の外部にある場合
3番目の証明では、以下のように∠APBが中心Oの外部になるような位置に点Pをとった場合を考えます。
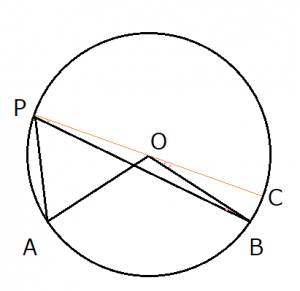
この証明ですが、1,2番目と違って少しややこしくなります。
まず前提として、点Pと中心Oに対して直線を引き、円周との交点をCとします。円周角は∠APB、中心角は∠AOBです。
上の画像より
∠APB=APO-BPO…①
となります。
次に三角形の外角定理を使うのですが、まず△APOに対して使います。
∠AOC=∠OPA+APO
さらに△APOは「OP=OA」から二等辺三角形になるので、
∠OPA=APO
になります。
すなわち
∠AOC=2∠APO…②
となります。
さらに三角形の内角の和は180度なので、
2∠APO=180-∠POA=∠AOC
∠POA=2(90-∠APO)…③
となります。
さらに∠POAに関しては、
∠POA=180-∠AOB-BOC…④
となりますが、∠BOCは△PBOが二等辺三角形でかつ外角定理より
∠BOC=2∠BPO
となるので、これを④式に代入すると
∠POA=180-∠AOB-∠BOC=180-2∠BPO-∠AOB
③式も代入して両辺をまとめると
2(90-∠APO)=2(90-∠BPO)-∠AOB
∠APO=90-90+∠BPO+1/2∠AOB=∠BPO+1/2∠AOB
∠APO-∠BPO=1/2∠AOB…⑤
①、⑤式より、
∠APO-∠BPO = ∠APB=1/2∠AOB
よって定理1が証明できました。
以上3つのパターンより、円周角が円周上のどの位置にあっても中心角の大きさが半分になること、及び同じ弧に対する円周角の大きさは全て等しいことが証明されました!
スポンサーリンク
直径に対する円周角は直角!
円周角の定理についての大きく分けて3つの証明パターンを紹介しました。
学校の授業でも習うと思いますが、三角形の内角の和や外角定理なども出てきて凄く重要なポイントだと思います。
また円周角の定理はこの他にも以下のように、弧ABがちょうど半円、即ちABがちょうど直径になる時の円周角が直角になることも頭に入れておきましょう!

これはタレスの定理と言われていて、円周角の定理の応用です。
証明は凄く簡単で、要は中心角が180度になるので、円周角がその半分、即ち90度になるだけということです。
言われてみれば何のことはないと思いますが、試験に出やすいポイントと言えます。またこの直角三角形になることが非常に重要で、実は三平方の定理の証明にも使われます。
詳しくは以下の記事をどうぞ!
三平方の定理の証明!中学生向けの方法を6つ紹介!
円周角の定理の逆とは?
円周角の定理では証明も大事な事柄ですが、逆が成立することも大事な要素です。
2つの点C,Dが直線ABにおいて同じ側にある時、∠ACB=∠ADBならば、4つの点A,B,C,Dは同一円周上にある。
この性質も試験に非常に出題されやすいので、是非とも覚えておきましょう!
ではどういった感じで出題されるのか?具体例を出して解説します。
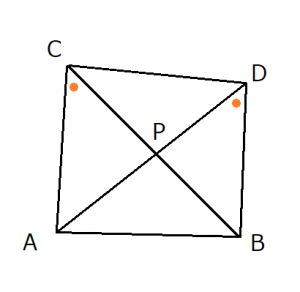
∠ACB=50度、∠DBC=60度だったとします。また線分ADと線分CBの交点をPとします。
この時、∠APCの大きさを求めよ。
こういった感じで出題されます。
まず円周角の定理より∠DBC=∠CADが言えるので、
∠CAD=60
になります。
続いて三角形の内角の和より、
∠APC=180-∠ACB-∠CAD=180-110=70
よって70度となります。
ここでちょっとした応用テクニックを教えます。
上の画像を見てもらえれば、円周角は∠ACBと∠CADだけでなく、∠CDAが弧CAの円周角、∠BADが弧BDの円周角になっていますね。
そしてこれら4つの円周角がそれぞれ2つずつあり、四角形ABCDの4つの角を形成しています。
これらのことから以下のことが成立します。
(4つの円周角の和)×2=360度(四角形の内角の和より)
→4つの円周角の和=180度
→∠ACB+∠CAD+∠CDA+∠BAD=180
これも覚えていれば試験に役立つでしょう。
逆の証明は?
円周角の定理の逆はなぜ成立すると言えるのでしょうか?
これは高校数学の話も少し絡んでくるのですが、ある命題(この場合「円周角の定理」)の逆は必ずしも成り立つとは限りません。
なので円周角の定理の逆はまた別個に証明しないといけません。
ではその証明法ですが、以下の画像のように4つの点の内のDの位置をいろいろ変えて考えます。
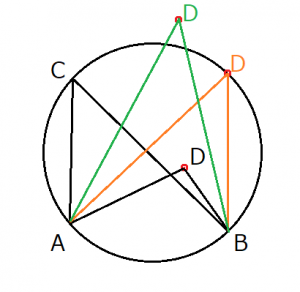
- Dが円の内部にある
- Dが円周上にある
- Dが円の外部にある
この3パターンを考えた時に、ABと点Dとの間になす角の大きさはそれぞれ以下のようになります。
- ∠ACB<∠ADB
- ∠ACB=∠ADB
- ∠ACB>∠ADB
以上より∠ACB=∠ADBということは、Dが円周上にあることと同値になるので、円周角の定理の逆が成り立つことが証明できました。
この証明も応用ですが、覚えておいて損はないでしょう。
まとめ
今回は円周角の定理の証明と逆についての解説でした。
円周角の定理の証明は完璧でも、意外と逆について把握していなかったという人も多いとでしょう。
基礎的な内容ですが高校数学の図形問題でもよく出てきます。復習は完璧に!
【こちらの記事もどうぞ!】
同じ誕生日の人がいる確率の計算!50%以上になる人数は何人?
スポンサーリンク
