三平方の定理といえば皆さんも学校の数学の授業で習うでしょう。
ご存知直角三角形の斜辺の長さを求める時に使われる公式ですね。
発見した数学者の名前をとってピタゴラスの定理とも言われています。

しかし改めてですが、なぜこの定理が成り立つのか?少し疑問ですね。
恐らく証明についても多くの学校で習うと思いますが、あまり重要視されず習ってもそのまま忘れる人は多いです。
ただいざ試験に出てきたらと思うとちょっと怖いですよね(;^^)
もちろんこの定理を使って辺の長さを求めるパターンが多いですが、いざ出てきた時のことを考えて復習の意味も込めて詳しく解説していきます!
※証明法はいくつかあるのですが、今回は中学生までの範囲で解けるパターンのみ紹介することにします。
スポンサーリンク
三平方の定理の証明
三平方の定理とは以下のように直角三角形ABCがあった時に、辺a(底辺)と辺b(高さ)の2つと辺c(斜辺)の関係性を以下のような等式で表した定理です。
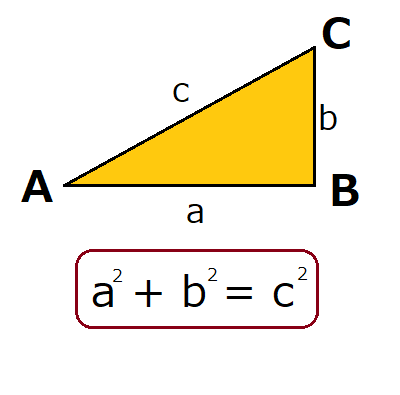
公式:a²+b²=c²
わかりやすく文章で表現しますと、底辺の2乗と高さの2乗の和が斜辺の2乗に等しいことです。
二乗になるので最終的には平方根(√)をつければ斜辺が求まります。
つまり底辺と高さの2つの長ささえわかれば、斜辺の長さがわかることになるわけですね。
なぜこのような公式が成り立つのか?その証明について今回は以下の5つのパターンに分けて解説していきます。
- ピタゴラスの証明
- バースカラ2世の証明
- ガーフィールドの証明
- 相似を使った証明
- 等積変形を使った証明
まず一番代表的なピタゴラスが用いた証明から紹介していきます。
ピタゴラスが用いた証明法
三平方の定理の証明といえば、一番メジャーな方法がこれではないでしょうか?
発見者ピタゴラス自身が用いた証明方法です。数学の教科書にもちゃんと書かれていますので知っている人は多いでしょう。
その証明手順を解説しますと、以下のように正方形の中に小さな正方形を入れた図形を用意します。
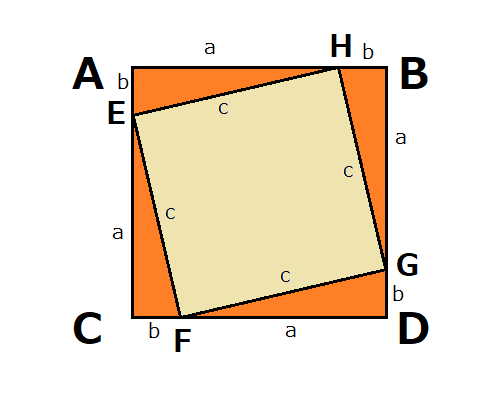
大きな方の正方形をABCD、小さい方の正方形をEFGHとします。
よく見ると大きな方の正方形ABCDの四隅にそれぞれ大きさが同じの直角三角形が4つ出来ていますね。
ここで自ずと以下の等式が成り立ちます。
また上の画像より、正方形ABCDの一辺の長さは a+bなので、面積は(a+b)²となります。
次に正方形EFGHの面積はc²、4つの直角三角形の面積は(ab)/2なので、これらを上の等式に代入すると、
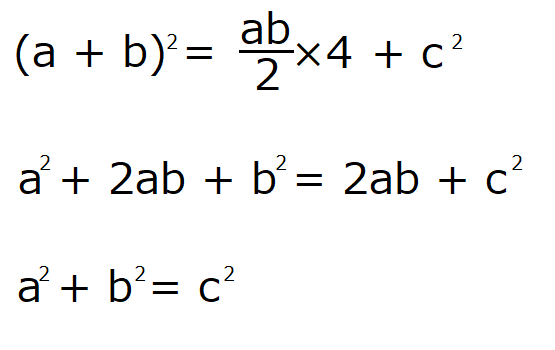
となるのがわかります。これを解けば見事三平方の定理の完成です!
バースカラ2世の証明法
以下のように正方形ABCDの中に小さい正方形が入っている図形を想定するのですが、ピタゴラスとの違いは4つの直角三角形の斜辺の長さが正方形ABCDの一辺と等しくなっていることです。
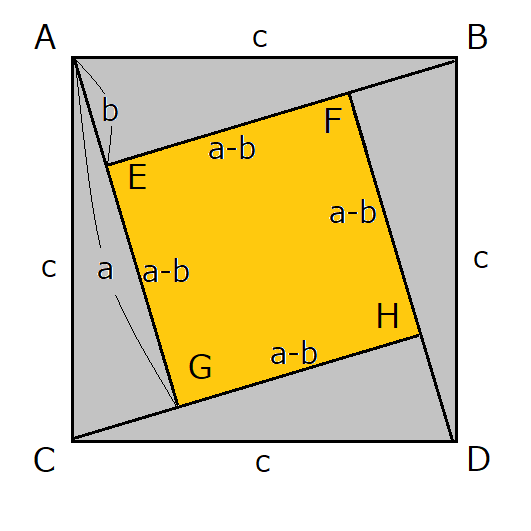
上のようにして敷き詰めると、ちょうど真ん中に小さな正方形が出来上がりますね。
この小さい正方形を仮に正方形EFGHとします。
また4つの直角三角形の斜辺をc、底辺をa、高さをbとすると、ちょうど真ん中の正方形EFGHの一辺の長さが a-b となることがわかります。
(EG = AG - AE = a - b)
ここでピタゴラスの時と同様に、正方形ABCDと4つの直角三角形と正方形EFGHの面積から三平方の定理を導きます。
上の画像から、
となるので、式で表すと
c² = {(ab)/2}×4 + (a – b)²
c² = 2ab + a² -2ab + b²
c² = a² + b²
よって三平方の定理が導けました!
ガーフィールドの証明
なんとアメリカ合衆国の大統領もこの定理の証明に挑戦していました!
この証明法を導いたのは第20代合衆国大統領ジェームズ・ガーフィールド氏です。相当な頭脳の持ち主だったんですね、何で大統領になったのやらwww
ガーフィールドの証明は、以下のような台形と合同な直角三角形を用いた画期的な方法でした。
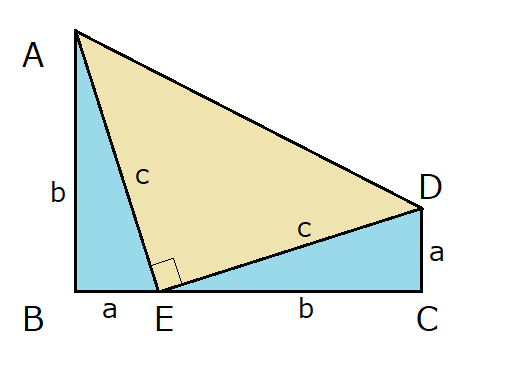
おさらいしておくと台形の面積は、
{(上底+下底)×高さ}/ 2
でしたね。
やはりこの証明にも鍵となるのは面積です。上の画像では2つの合同な直角三角形がありますが、よく見ると両辺がcで同じ長さの直角二等辺三角形もありますね。
※∠AEDが90度になるのは、三角形の外角定理より導けます。
すなわち2つの直角三角形(△ABEと△CED)と直角二等辺三角形(△AED)の面積の和が、台形の面積と等しくなるので、
2×(ab)/2+(c²)/2=(a+b)²/2
2ab+c²=(a+b)²
2ab+c²=a²+2ab+b²
これを解けば見事三平方の定理の完成です!
スポンサーリンク
相似を使った証明
相似を使った証明方法には2通りあります。その前に相似について簡単に復習しましょう。
2つの三角形が相似である条件は、以下の3つの内どれか1つを満たせばよい。
| 二組相等 | 2組の角の大きさが等しい時 |
|---|---|
| 三辺比相等 | 3組の辺の比が互いに等しい時 |
| 二辺比夾角相等 | 2組の辺の比とその間の角の大きさがそれぞれ等しい時 |
直角三角形の直角から垂線を下ろす
以下のように直角三角形ABCがあったとして、直角となる頂点Bから辺ACへ垂線を下ろします。
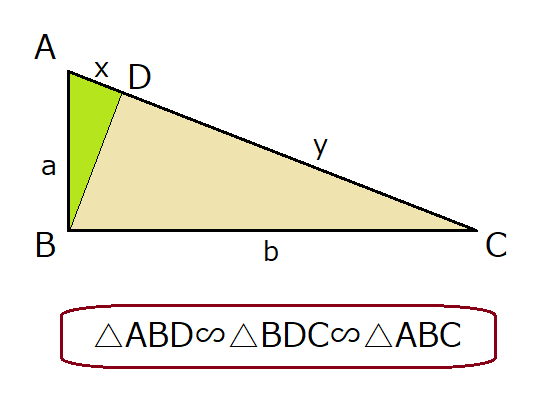
この時、辺ACと垂線との交点をDとし、AD=x、DC=yとすると、
AC=x+y=c…①
となります。
ここで三角形の相似を利用します。
上の画像をよく見てみると、3つの直角三角形(△ABDと△BDCと△ABC)が隠れていますが、それぞれ直角でかつ1つの角を共有しているので相似となっています。
相似ということは、2つの辺の比が等しいことも意味します。まず△ABDと△ABCの2つより、
AB:AD=AC:AB
a:x=c:a
cx=a²…②
となります。
次に△BDCと△ABCの2つより、
BC:DC=AC:BC
b:y=c:b
cy=b²…③
①と②と③の3式より、
a² + b² = c(x+y)=c²
となって三平方の定理が完成します!
半円を用いた証明
相似を用いた証明には半円を用いた別のやり方も存在します。
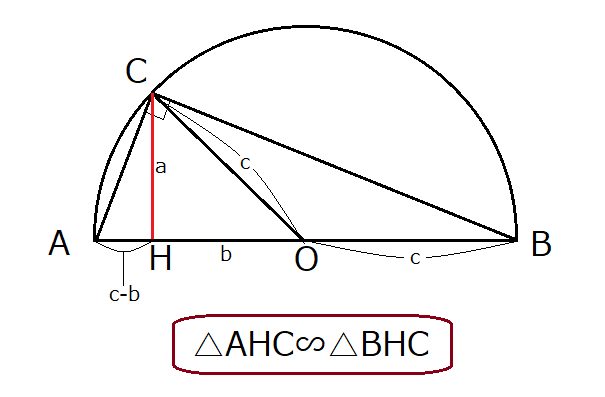
上の画像では直径ABの半円Oで、円周上に置いた点Cから直径ABに垂線を下ろしその交点をHとします。
OAとOBとOCは円の半径なので全てc、HC=a、OH=bとします。
すると△AHCと△BHCが相似になるので、辺の比の等式から以下のようにして三平方の定理が導けます。
HA:HC=HC:HB
OA-OH:HC=HC:OB+OH
c-b:a=a:c+b
a²=(c-b)(c+b)
a²=c²-b²
a²+b²=c²
等積変形を用いた証明
等積変形とは以下のように平行線があった時に、赤く塗った三角形ABCの頂点Cを移動させても面積が等しくなる性質のことを言います。
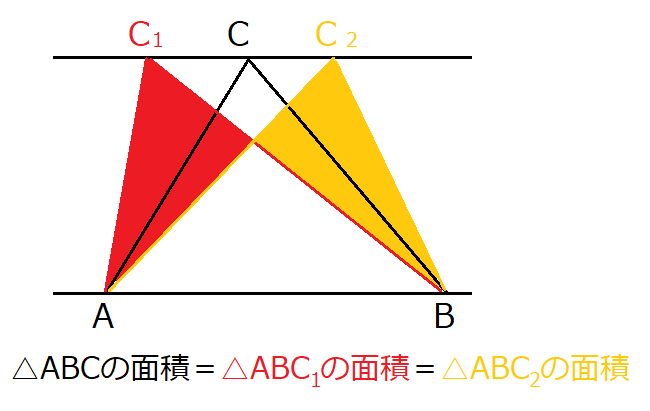
頂点Cをどこに移動させても、底辺と高さ自体は変わらないので必然的に面積は等しくなります。
この等積変形を用いることでも三平方の定理を証明できます。前提として以下のような図形を用意します。
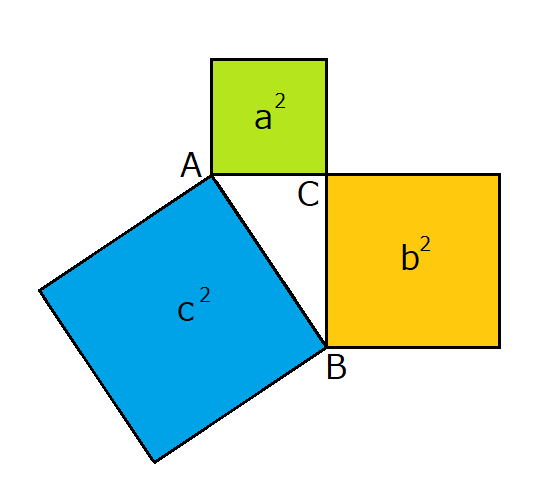
直角三角形ABCがあった時に、辺ACと辺ABと辺CBの長さに等しい正方形を3つ直角三角形にくっつけます。
ここで重要となるのが、斜辺ABで作られた正方形の面積です。
三平方の定理の思い出してみると、底辺aの2乗と高さbの2乗の和が斜辺cの2乗に等しい、でしたね。
これは言い換えてみたら、1辺の長さがaの正方形の面積と1辺の長さがbの正方形の面積の和が、1辺の長さがcの正方形の面積と等しいことでもあります。
上の画像で見ると、緑色の正方形の面積と橙色の正方形の面積の和が青色の正方形の面積と等しくなることです。
これを等積変形で証明してみせます。
まず緑色の正方形、橙色の正方形、それぞれ以下のように半分に分けます。
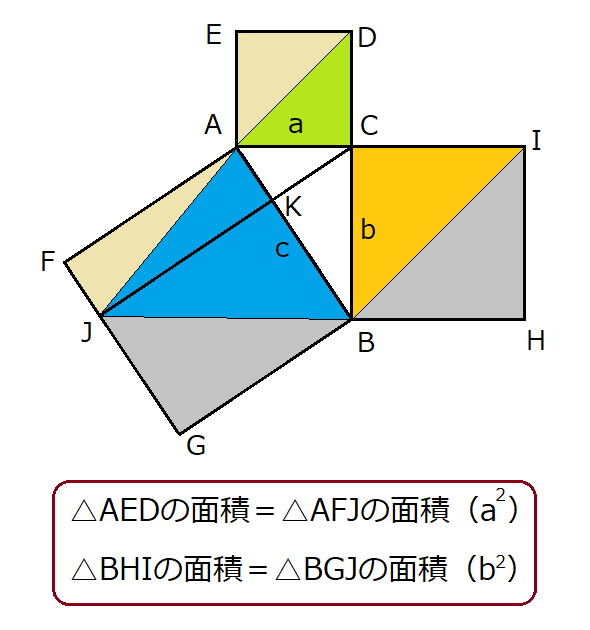
この時辺AEと辺BDが平行線になっていることに注目です。これにより緑色の正方形で半分に分けた△AEDの面積は、等積変形で△AEBと等しくなります。
同様に橙色の正方形についても、辺BHと辺AIが平行なためやはり等積変形が使えます。
この2点より、以下の2つの等式が成り立ちます。
- △AED=△AEB
- △BHI=△BHA
次に△AEBにおいては、以下の3点が成り立つため△ACFと合同になります。
- AE=AC(正方形だから)
- AB=AF(正方形だから)
- ∠EAB=∠CAF
さらに頂点Cから辺FGに下した垂線との交点をJとすると、△ACFと△AFJがやはり等積変形で面積が等しくなります。
最終的に、
△AEDの面積=△AFJの面積
となります。
また頂点Cから辺ABに下した垂線との交点をKとすると、△AFJは長方形AFJKの半分になっていることがわかります。
よって△AFJの面積の2倍が長方形AFJKの面積と等しくなります。
これと全く同じ要領で橙色の正方形の半分にした△BHIが、今度は長方形BGJKの半分になっていることがわかります。
やはりこちらも△BHIの面積の2倍が長方形BGJKの面積と等しくなります。
以上より
(2×a²)/2 + (2×b²)/2 = 長方形AFJKの面積 + 長方形BGJKの面積 = 正方形AFGBの面積 = c²
となるので、これを解けば三平方の定理の等式が完成します!
まとめ
今回は三平方の定理の証明を6つほど紹介しました、参考になりましたら幸いです!
高校数学になるとベクトルや積分を使っての証明もあって、より深くピタゴラスの定理の証明について学ぶことができます。
また三平方の定理は単に図形で辺の長さを求めるだけならず、いずれは物理学や電気工学にも応用する大事な基礎理論です。この機会にしっかりと定理について復習して見直しましょう!
【こちらの記事もどうぞ!】
素数が無限に存在することの証明!高校数学の知識と応用編も紹介!
スポンサーリンク
