今回は知る人ぞ知る、有名な問題を紹介します。
まず真北に1km進み、
次に真東に1km進み、
そして真南に1km進むと、
なんと自宅に戻ってきてしまいました。
なぜでしょう?
という問題です。
もちろん家がものすごく大きかったということではなく、また自宅が移動してきたということでもありません。
本当に元の位置に戻ってきた、ということです。
答えは、
家が南極点にあった。
となった方もいると思いますので、詳しく解説していきます。
スポンサーリンク
平面ではなく曲面で考える!
まずこの問題を考える前に、みなさんが普段思い浮かべる平面とはどんなものなのか考えます。
普通の2次元空間は縦と横に一様に広がっている平面ですね。この平面上では2つの直線が平行になっている場合、永遠に交わりません、永遠に平行のままです。
しかしもしもこの平面が曲がってしまったらどうでしょう。
平面を曲げて球体にまで変えたとき、2つの平行線はなんと交わってしまうのです。
そんな馬鹿な!? と思われるのも無理はありません。少なくとも多くの人は平行線は交わらない、と学校では教わりました。
しかしこれは、ユークリッド幾何学という世界での話。ざっくり言うと「どこまでも真っ平らな平面上」、「全くゆがみのない空間」の中での図形に関して言えることなのです。
小学校、中学校、高校と習ってきた算数と数学は全てユークリッド幾何学の世界です。
しかしこの常識が通用しない世界が、『非ユークリッド幾何学』です。
先ほどの問題は極端な例と言えますが、仮に南極点にいなくとも、我々人類が住んでいる地球はまさに球体です。
みなさんも世界地図は何度も見たことはあると思いますが、縦に何本も経線が走っているのはよくご存じだと思います。しかしこの経線は全て南極点と北極点で1点に交わります。
普段見る地図は平面でしか表現できないので、平行線で交わりそうに見えませんが、実際は球体なので1点に交わるのです。
非ユークリッド幾何学の面白さとは!?
非ユークリッド幾何学についてもう少し面白い話があります。
三角形の内角の和は180度というのも、中学校で習う知識なのでよくご存じだと思いますが、実は非ユークリッド幾何学、球面上で三角形を作成した時は内角の和は180度とはならないのです。直感的に考えれば三角形自体が膨らむので多少イメージできると思います。
またそれ以外にも通常の平面では実現できない二角形なんかもこの非ユークリッド幾何学の場合なら実現可能になります!
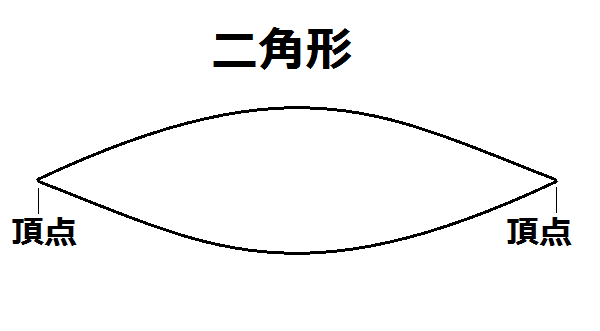
地球儀を持っている方は紙を貼ってみて、その上から鉛筆でなぞってみれば意外と簡単に描けます、ぜひお試しください!
こんな感じで今まで学んできた数学の知識や常識が通用しないのが非ユークリッド幾何学の面白いところでもあります。興味が湧いてきた人は、大学の理学部に進学すればもっと詳しく学べますよ!
関連記事
スポンサーリンク
